Many problems in computer graphics are a translation of an input image into a corresponding output image. For example, performing colorization of a black and white image, converting horses to zebras, classifying pixels on an image (image segmentation) and similar. This article will cover two very interesting approaches based on generative adversarial networks - GANs [1, 2, 3]. We will also assume that the reader is familiar with GANs, so make sure to refresh your memory on the topic [1].

Traditionally, the image translation problem has been tackled with many different techniques depending on problem conditions, available data, and domain (RGB to semantic map, black-white to RGB...), but essentially it can be said that the goal of image translation problem is to predict output pixels from input pixels [2].

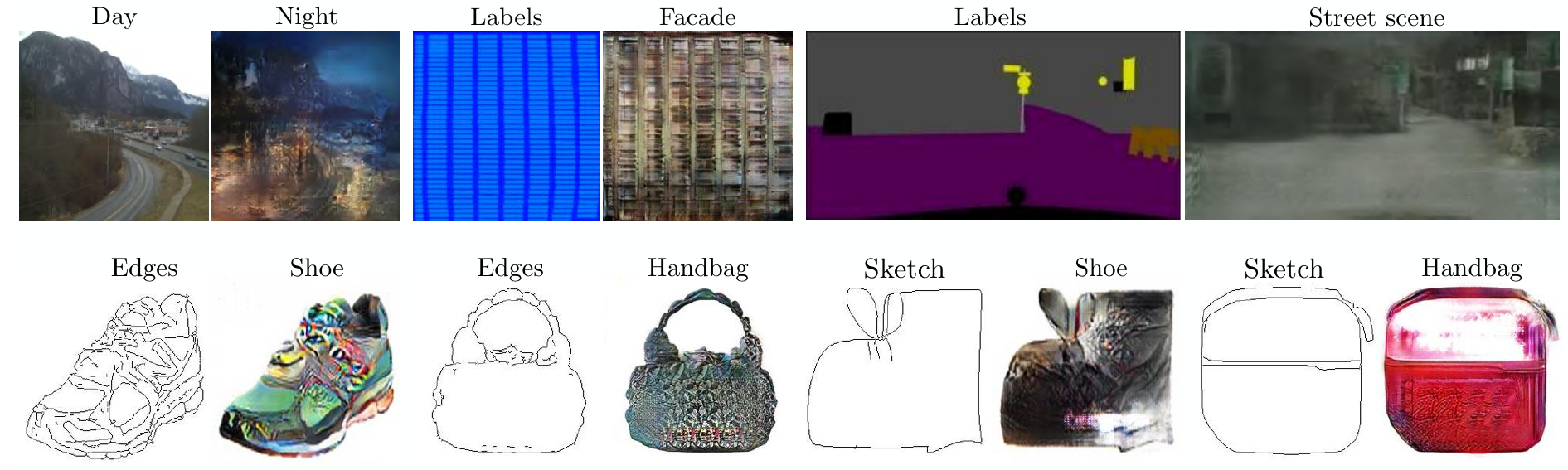
The following image shows some examples of image translation problems.

This article will mainly cover the following two papers:

• Image-to-Image Translation via Conditional Adversarial Networks [2] - Pix2pix
• Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks [3] - Cycle GAN

Images used in this article are taken from [2, 3] unless otherwise stated.

Image-to-Image Translation via Conditional Adversarial Networks - Pix2pix

The paper examines an approach to solving the image translation problem based on GANs [1] by developing a common framework that can be applied to many different forms of problems in which paired training data is available. As GANs have a generator $G$ and a discriminator $D$, the main goal of the generator is to learn how to transform an image $a$ from domain $A$ into an image $b$ from domain $B$ and the goal of the discriminator is to try to classify whether the input image was created by the generator or it came from the available dataset.

Pix2pix makes the assumption that paired data is available for the image translation problem that is being solved. In contrast to that, Cycle GAN, discussed in later parts of this article, is created in order to support working with unpaired data.

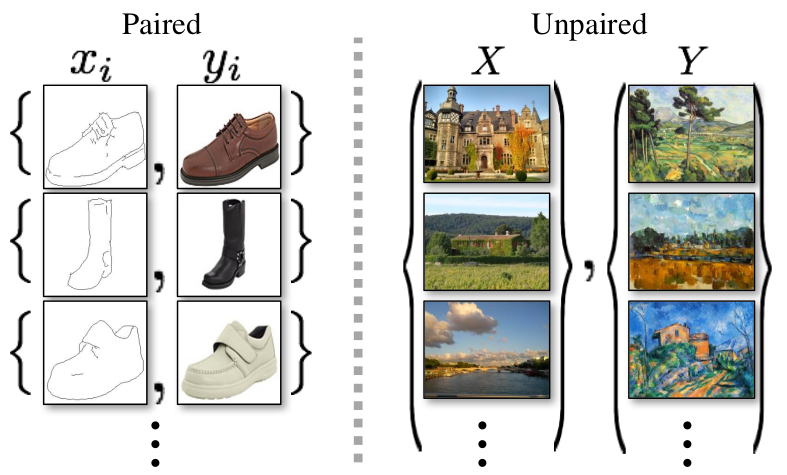
Having paired data also allows Pix2pix to additionally constrain the learning process by conditioning discriminator on the input image. To accomplish this, conditional GANs (cGANs) are used [4].

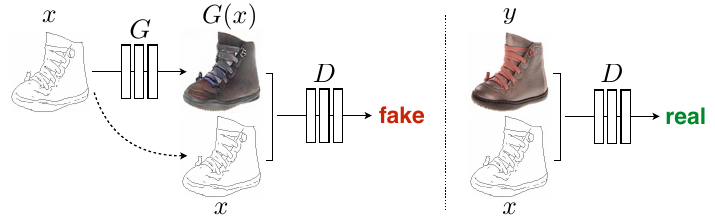
Training is accomplished by optimizing the following objective:

$$
\mathcal{L}_{cGAN} (G, D) = \mathbb{E}_{x, y} \Big[ \log D(x, y) \Big] + \mathbb{E}_{x, z} \Big[\log (1 - D(x, G(x, z))) \Big]
$$

Generator G tries to minimize this objective against an adversarial D that tries to maximize it.

$$
G^* = arg \min_G \max_D \mathcal{L}_{cGAN} (G, D)
$$

For research purposes, the paper also tries a variant of the mentioned loss without conditioning.

$$
\mathcal{L}_{GAN} (G, D) = \mathbb{E}_{y} \Big[ \log D(y) \Big] + \mathbb{E}_{x, z} \Big[\log (1 - D(G(x, z))) \Big]
$$

Some papers have shown that mixing the GAN objective with a traditional loss (like $\ell_1$ and $\ell_2$) can be beneficial during the learning process [5]. This forces the generator not only to try and fool the discriminator, but also to try and be as close to the input sample on a pixel level in $\ell_1$ or $\ell_2$ sense. This makes sense in case when paired data is available due to images sharing a part of structure like black and white photos compared to the colored photo.

$$
\mathcal{L}_{L1} (G) = \mathbb{E}_{x, y, z} \Big[ ||y - G(x, z)||_1 \Big]
$$

Putting it all together:

$$
\mathcal{L}_{cGAN} (G, D) = \mathbb{E}_{x, y} \Big[ \log D(x, y) \Big] + \mathbb{E}_{x, z} \Big[\log (1 - D(x, G(x, z))) \Big]
$$

$$
\mathcal{L}_{GAN} (G, D) = \mathbb{E}_{y} \Big[ \log D(y)\Big] + \mathbb{E}_{x, z} \Big[\log (1 - D(G(x, z))) \Big]
$$

The final objective for optimization is as follows:

$$
G^* = arg \min_{G} \max_{D} \mathcal{L}_{cGAN} (G, D) + \lambda \mathcal{L}_{L1} (G)
$$

Model and architecture

Generator and discriminator architectures are adapted from [6]. Some of the important things to mention are:

• Generator uses skip connections
• Discriminator works on patches

Generator

Image-to-image translation problems often map a high-resolution image to a different high-resolution image. Having a traditional bottleneck layer in the generator can force it to learn a complex mapping between input-output, even though this is not required if images are sharing overall structure. For example, in image colorization problems (converting black-white images to colorized images) there is no need to encode-decode the structure and texture of the image as they are almost identical.

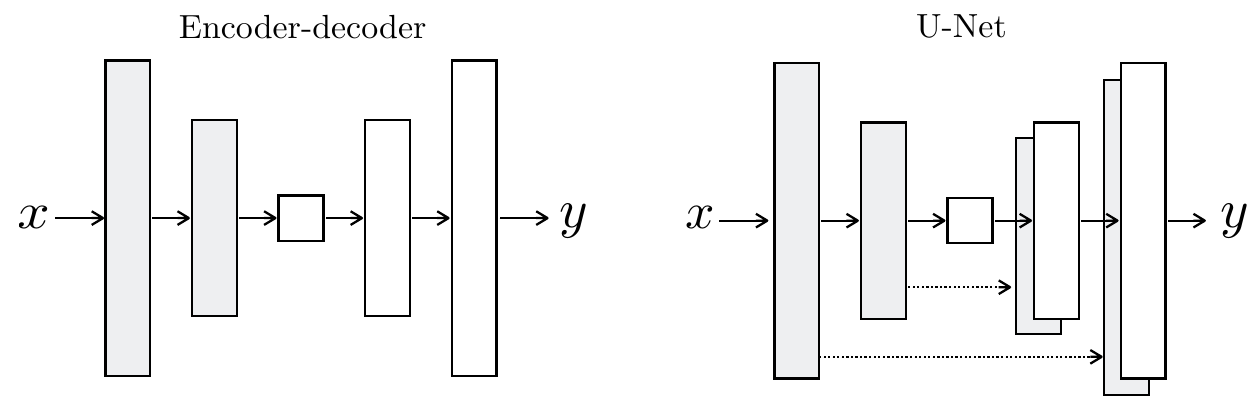
The importance of skip connection is best illustrated in the following image.

Adding skip connections to the encoder-decoder structure of the generator drastically improves the quality of generated images. The image also shows the impact of using only $\ell_1$ loss compared to the full objective defined for Pix2pix.

Discriminator and PatchGAN

The general idea is that in order to enforce proper structure and texture generation, patches of the input image are good enough. This is also good because it reduces inference computation complexity, which can improve overall GAN training time. Discriminator works on patches of an input image. The input image is downsampled, and every pixel of this new feature map is classified. The pixels that are classified are representing patches of the original image, while the size of the downsampled feature map is a meta parameter introduced by the Patch GAN.

Patch GAN was evaluated on images of size $286\times286$ and patches of size:

• $1\times1$ (called Pixel GAN)
• $16\times16$
• $70\times70$
• $286\times286$ (called Image GAN)

The following image illustrates the influence of different patch sizes.

Patch size of $1\times1$ increases the colorfulness of results but doesn't influence spatial sharpness. Increasing patch size to $16\times16$ improves on increasing spatial sharpness, but artifacts also start appearing. Moving to $70\times70$ improves results quite a bit - artifacts are reduced and spatial sharpness is increased. Increasing patch size to the full image size - $286\times286$ gives very similar results.

More details on overall model architecture can be found in the original paper.

Training

The paper reports nothing new concerning the training phase compared to the classic GAN training techniques developed earlier. The loss is optimized by altering updates to the generator $G$ and the discriminator $D$ during the training phase. The classic trick from [1] is used also as the objective function is modified by changing $\min \log \Big(1 - D(x, G(x, z))\Big)$ to $\max \log\Big(D(x, G(x, z)) \Big)$. The objective is divided by 2 while optimizing $D$ in order to slow down the rate of which $D$ learns relative to $G$ Adam optimizer is used with learning rate set to $0.002$ and $\beta_1 = 0.5$ and $\beta_2 = 0.999$.

Experiments and results

Some problems examined in the paper are:

• Semantic labels to photo (inverse of semantic segmentation)
• Architectural labels to photo
• Map to an aerial photo
• BW to color photos
• Edges to photo
• Sketch to photo
• Day to night
• Thermal to color photos
• Photo with missing pixels - inpainted photo

Paper also gives an ablation study of the components of the loss function and tries to reason on how do components of this function influence the final model.

$$
G^* = arg \min_{G} \max_{D} \mathcal{L}_{cGAN} (G, D) + \lambda \mathcal{L}_{L1} (G)
$$

From the photo it can be seen that $\ell_1$ alone gives reasonable but blurry results. As for the situation with $\mathcal{L}_{cGAN}$ loss, results improve but artifacts appear. Combining the previous two reduces the frequency and intensity of artifacts.

Detailed results are available here. Some nice results can be obtained even on small datasets:

• Facade training set consists of just 400 images, trained under 2 hours on a single Pascal Titan X GPU
• Day to night training set consists of 91 images

Map to the aerial photo (and inverse)

Image colorization

Cityscapes labels to photo

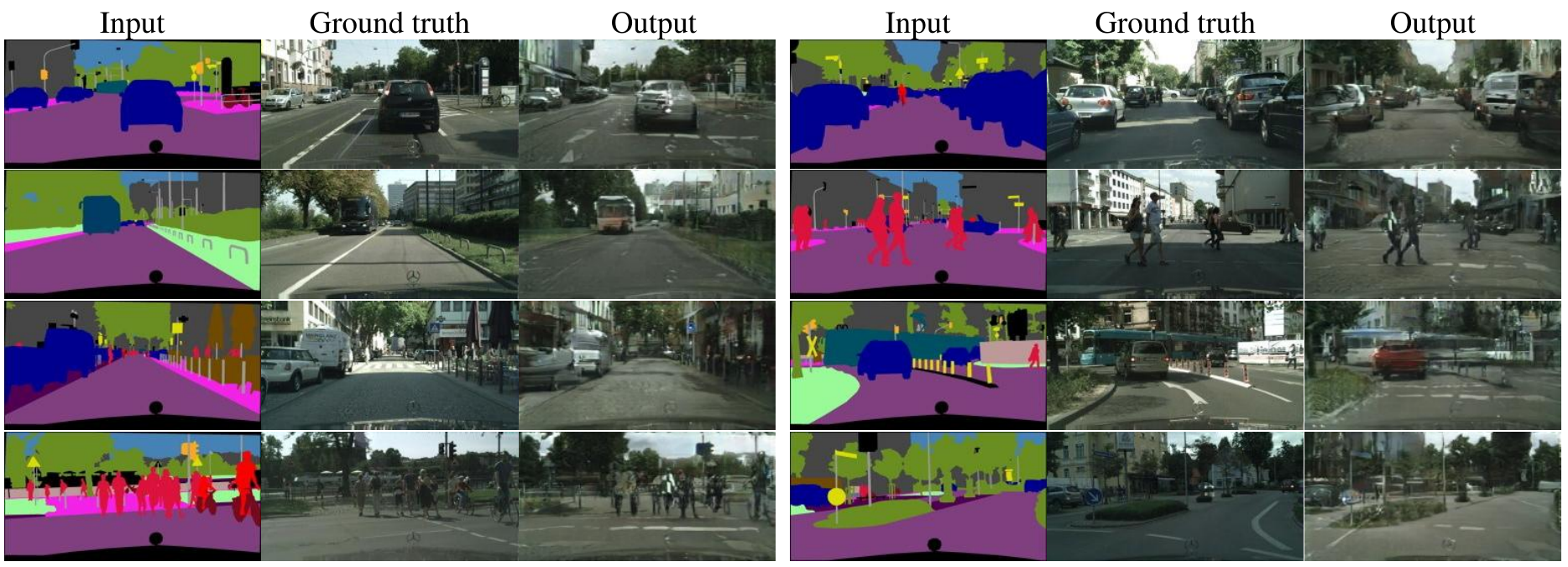
Facade labels to photo

Sketch to photo

Sketch to photo

Sketch to photo

Image inpainting

Thermal to photo

Removing background

Examples of failure

By using the fixed-size patch approach, the system can be adapted to work on varying image sizes. For example, it can be trained on $256\times256$ images and tested on $512\times512$.

Evaluation of synthesized images is an open and difficult problem because traditional metrics like pixel mean-square error do not capture concepts and structure. Paper employs 2 strategies for such evaluation:

1. Holistic approach
2. Using externally trained classifiers on synthesized images

Holistic approach relies on humans doing real vs fake studies over Amazon Mechanical Turk (AMT). The other approach uses a pre-trained semantic segmentation model like FCN-8s [7] that is used to classify synthesized images when labels are available for comparison.

Pix2pix and the community

Since the publication of the paper, the community has had fun! Some nice and funny use-cases were introduced:

• Transforming edges to cats
• Transforming sketches to pokemon
• Transforming sketches to portraits
• Generating color palettes
• Removing background
• Learning to see: Gloomy Sunday - video

Conclusion

Conditional GANs have performed well on paired image to image translation problems. Approach that Pix2pix has introduced is general enough to fix most of the paired image to image translation problems. Introducing patches has also allowed for computational complexity to be reduced and using a U-net style generator has drastically improved the quality of generated images. It's important to note that applying the Pix2pix approach requires having paired data which sometimes isn't available. In the next part, we will cover the Cycle GAN model that improves on Pix2pix by working with unpaired data.

Cycle GAN - Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks

Having paired data available is actually rather rare and collecting such data can require a large amount of resources. There are special cases where paired data is naturally available like season change, segmentation problems, image colorization, but in general cases, it would be good to have an approach similar to Pix2pix that can also work with unpaired data.

The goal of this model is to produce results comparable to the Pix2pix paper, but still be able to learn without requiring paired data. This is exactly what Cycle GAN does [3]. It builds upon the work from Pix2pix by introducing cyclic learning in the optimization process.

Cycle GAN approach

In Pix2pix, model $G$ was trained to translate images from domain $X$ to domain $Y$. Cycle GAN does the same, but additionally it also trains a model $F$ that translates images in the opposite direction - from domain $Y$ to domain $X$.
This introduces a cycle, hence the name, Cycle GAN.

Back-translation is a concept in which after translating from A to B, there is another translation process from B back to A in order to check how close is the original content compared to the one that went through the translation process. There is also an interesting story about Mark Twain and his work The Celebrated Jumping Frog of Calaveras County.
After discovering the French translation of his text and noticing how much of his signature humor and style were lost, Twain re-translated the French version word for word with intentional incoherency back into English with a new title The Jumping Frog: In English, Then in French, and Then Clawed Back Into A Civilized Language Once More by Patient, Unremunerated Toil to illustrate the problem of losing deep and subtle semantics during the translation process.

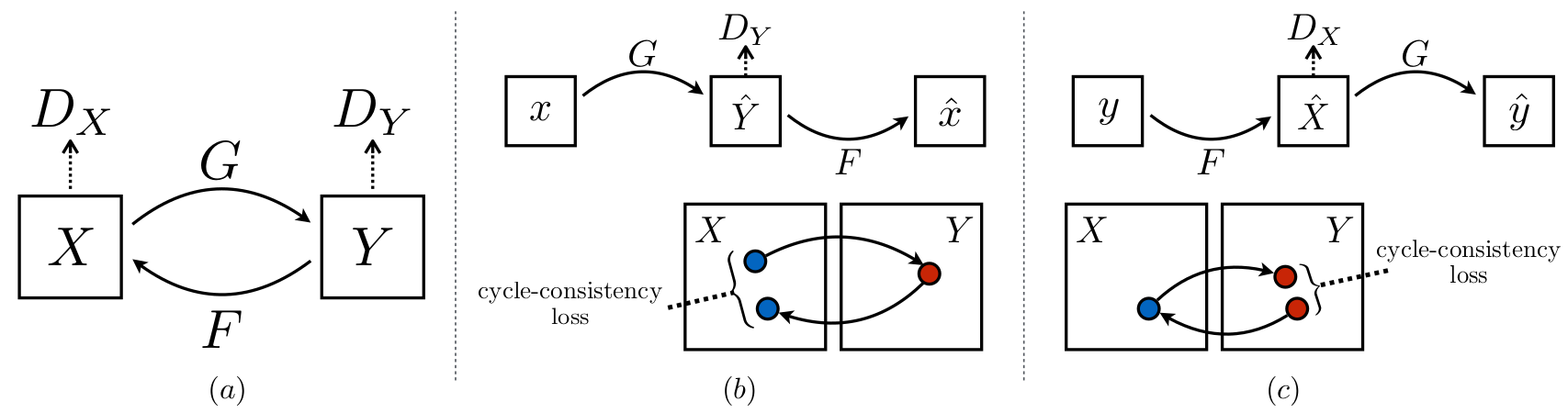
Cycle GAN consists of:

• 2 generators - $F$ and $G$
• 2 discriminators - $D_X$ and $D_Y$
• 2 additional losses:
  • forward cycle-consistency loss: $x \rightarrow G(x) \rightarrow F(G(x)) \approx x$
  • backward cycle-consistency loss: $y \rightarrow F(y) \rightarrow G(F(y)) \approx y$

Cycle GAN learns mapping functions between two domains, $X$ and $Y$. The available training samples are available ${x_i}^N_{i=1}$, $x_i \in X$ and ${y_i}^M_{i=1}$, $y_i \in Y$. Generator $G$ is tasked with the job of converting samples from domain $X$ to $Y$, while generator $F$ does the opposite, converting samples from $Y$ to $X$. Discriminators $D_X$ and $D_Y$ perform binary classification in which they try to determine whether samples belong to the domain $X$ and $Y$, respectively.

Objective consists of:

• Adversarial loss: $\mathcal{L}_{GAN} (G, D_Y, X, Y)$ and $\mathcal{L}_{GAN} (F, D_X, Y, X)$
• Cycle consistency loss: $\mathcal{L}_{cyc} (G, F)$

Adversarial loss

Adversarial loss is applied to both $G$ and $F$. For generator $G$ and discriminator $D_Y$, it can be formulated as:

$$
\mathcal{L}_{GAN} (G, D_Y, X, Y) =
\mathbb{E}_{y \sim p_{data}(y)} \Big[ \log D_{Y}(y) \Big]
+ \mathbb{E}_{x \sim p_{data}(x)} \Big[ \log \big(1 - D_Y (G(x)) \big) \Big]
$$

$G$ tries to minimize this loss while discriminator $D_Y$ tries to maximize it. This can be
expressed as:

$$
\min_G \max_{D_Y} \mathcal{L}_{GAN} (G, D_Y, X, Y)
$$

It is similar for $F$ and $D_X$ and can be formulated as:

$$
\min_F \max_{D_X} \mathcal{L}_{GAN} (F, D_X, Y, X)
$$

The Cycle consistency loss

The cycle consistency loss tries to capture how different is the reconstructed sample from the original sample. For example, how different is the original story from Twain compared to the version that was translated from English to French, and then back to English?

The cycle consistency loss consists of:

• Forward cycle consistency: $x \rightarrow G(x) \rightarrow F(G(x)) \approx x$
• Backward cycle consistency: $y \rightarrow F(y) \rightarrow G(F(y)) \approx y$

The loss is then formulated as:

$$
\mathcal{L}_{cyc} (G, F) =
\mathbb{E}_{x \sim p_{data}(x)} \big[ \| F(G(x)) - x \|_1 \big] +
\mathbb{E}_{y \sim p_{data}(y)} \big[ \| G(F(y)) - y \|_1 \big]
$$

Full objective

The final loss function is expressed as:

$$
\mathcal{L} (G, F, D_X, D_Y) =
\mathcal{L}_{GAN} (G, D_Y, X, Y) + \mathcal{L}_{GAN} (F, D_X, Y, X) + \lambda \mathcal{L}_{cyc} (G, F)
$$

And the full objective is:

$$
G^*, F^* = arg \min_{G, F} \max_{D_X, D_Y} \mathcal{L} (G, F, D_X, D_Y)
$$

Training details

The training is executed in a traditional GAN style altering the generator and discriminator updates. In the paper the value of $\lambda = 10$ was used along with Adam optimizer with an initial learning rate of $0.0002$ and batch size of 1. The learning rate is fixed for the first 100 epochs, and then linearly decayed to 0 over the next 100 epochs. Discriminators use a $70\times70$ Patch GAN.

Evaluation

Cycle GAN seems to work rather well in experiments given in the paper. The following two images demonstrate how Cycle GAN performs compared to the earlier methods.

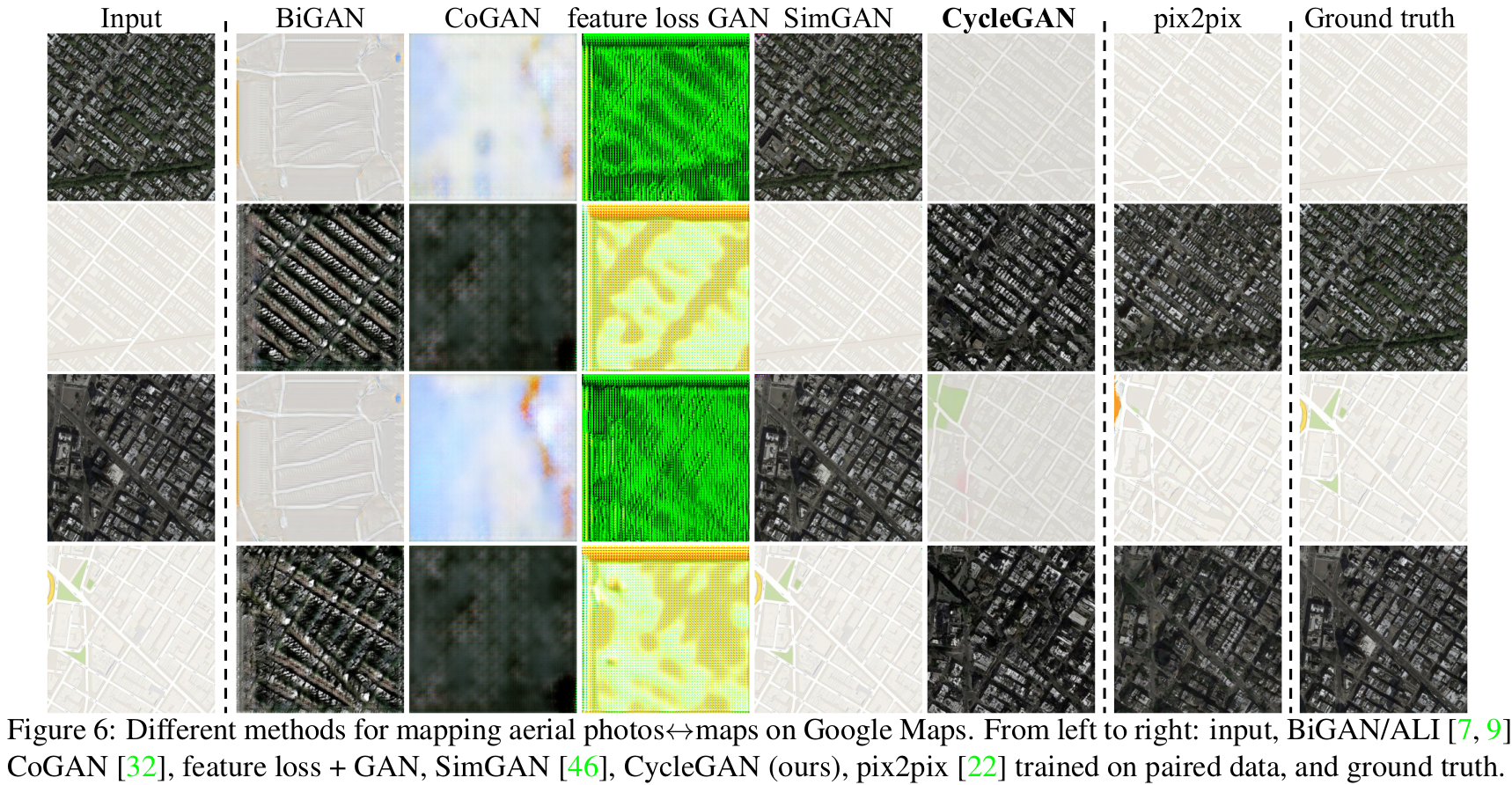
The paper reports the results of multiple experiments:

• unpaired image-to-image translation problems
• paired image-to-image translation problems
• with a focus on the importance of the cycle and adversarial loss
• with a focus on generality on different datasets

There was also an experiment done via Amazon Mechanical Turk (AMT) that has shown that images generated by Cycle GAN managed to make participants think they are real for around 25% of the time.

On paired image-to-image translation problems, Cycle GAN is comparable to Pix2pix:

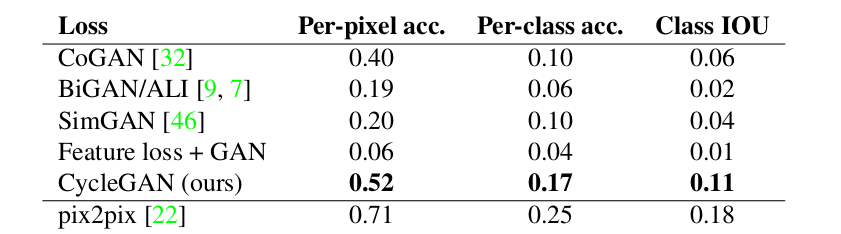
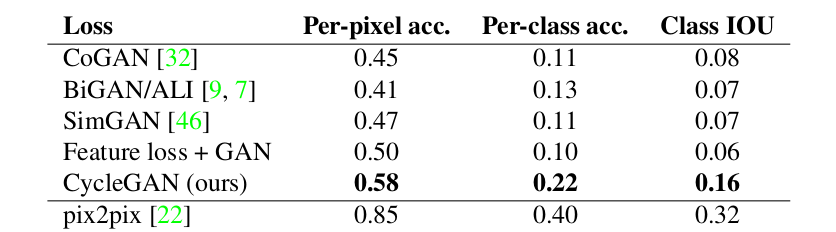
All parts of the loss function influence the quality of the model. The following image shows the classification performance of the photo-to-labels model for different losses, evaluated on Cityscapes.

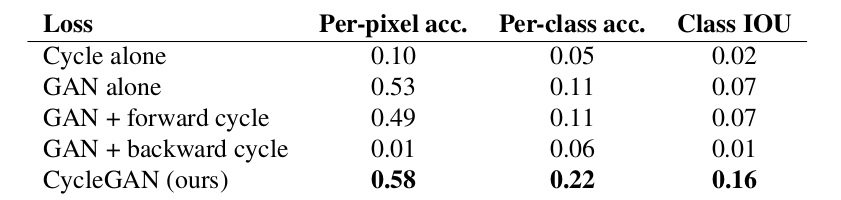
This can also be seen by visualizing the generated images.

Cycle GAN can be applied to the same problems as Pix2pix. The following few images show the obtained results.

Style transfer

Object transfiguration (horse to zebra)

Season transfer

Photo enhancement

Failure cases

Results are impressive in many of the previously shown images, but things can also fail to work due to many reasons - lack of data, mode collapse, special cases that are not present in the dataset and similar. The authors conclude that the model works rather well if it needs to learn a transformation which requires texture and color changes, but mostly breaks if it needs to learn geometrical transformation, like transforming a cat to a dog.

Conclusion

Cycle GAN has the ability to generate very good results for unpaired and paired data. One of the possible use cases very relevant to practical needs is learning a model to bridge the distribution gap between synthetic and real data in situations in which synthetic data is cheap and easy to get compared to the real data. It is also interesting how learning the inverse mapping can be used to allow the model to learn on unpaired datasets.

Although the results are really impressive, the regular GAN pain points like
mode collapse, unstable training and large amount of computational resources required still remain.

Resources

• [1] Generative Adversarial Networks, Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio
• [2] Image-to-Image Translation with Conditional Adversarial Networks, Phillip Isola and Jun-Yan Zhu and Tinghui Zhou and Alexei A. Efros
• [3] Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks, Jun-Yan Zhu, Taesung Park, Phillip Isola, Alexei A. Efros
• [4] Conditional Generative Adversarial Nets, Mehdi Mirza, Simon Osindero
• [5] Context Encoders: Feature Learning by Inpainting, Deepak Pathak, Philipp Krahenbuhl, Jeff Donahue, Trevor Darrell, Alexei A. Efros
• [6] Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks, Alec Radford, Luke Metz, Soumith Chintala
• [7] Fully Convolutional Networks for Semantic Segmentation, Jonathan Long, Evan Shelhamer, Trevor Darrell