Introduction

In this paper insight we discuss two recent papers that deal with the following problem: how to animate an image given a target video with motion in a self-supervised manner. This involves unsupervised keypoint detection, segmentation and optical flow estimation along the way. The discussed papers are:

• First Order Motion Model [1] - animating a source image based on the motion in a target video, using keypoints found in the image and in the video

• Motion-supervised Co-Part Segmentation [2] - animating segments of a source image based on the motion of the corresponding segments in a target video

We call the input image that we wish to animate the source image and the video with the movement we wish to imitate the target video.

The model in [2] can be seen as more general than [1] as one can simply replace all the segments in the target video with the segments in the source image. In fact, the motion co-segmentation model is trained starting from the pretrained weights of the first order motion model. Since both papers use similar architecture and ideas, in this post we mostly concentrate on [2] and comment on differences between [1] and [2] later on.

Motion-supervised Co-Part Segmentation

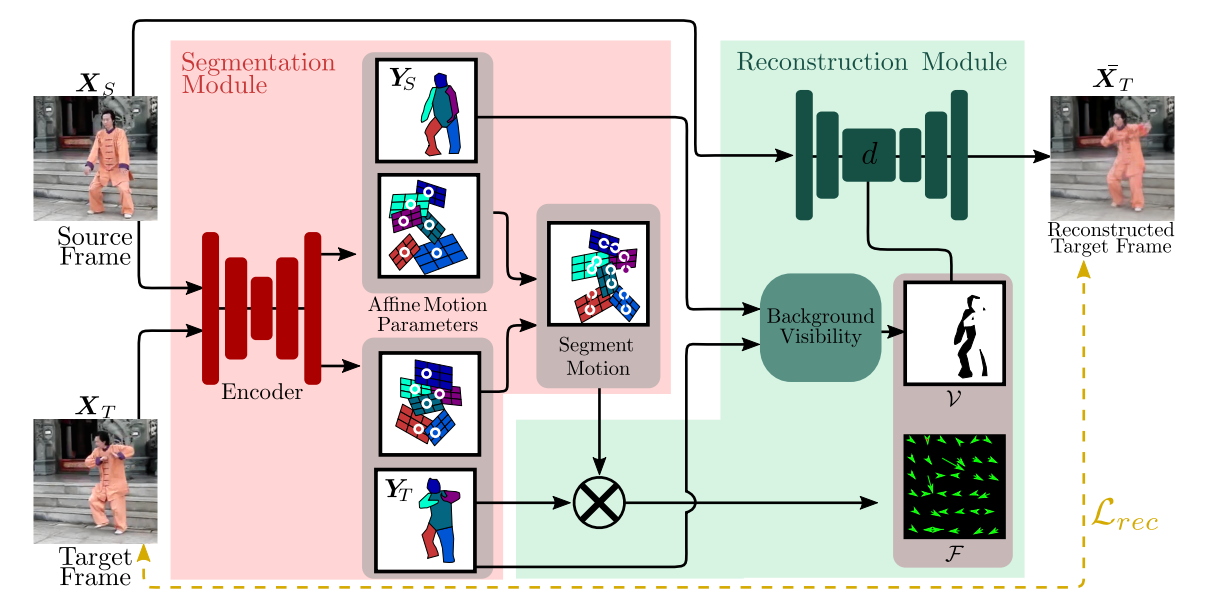
In a nutshell, the model takes in a source frame and a target frame, and outputs a reconstruction of the target frame using the source frame and "motion" between the source frame and the target frame. This is done by performing segmentation of both images and finding corresponding affine transformations between the segments.

Note that the model is trained only with videos, i.e with target frames taken from some video and source frames from the very same video. During inference, however, one may input any source frame and target frames to obtain a sequence of reconstructed target frames. The hypothesis is that if we have a source frame and a target video viewing an object consisting of similar segments, this will allow the target video to drive the source frame in a meaningful and consistent way. Except for consistent movement within segments, segmentation has one more application. One can select only certain segments to be reconstructed while using the original target frame otherwise. This makes it possible to do things such as face swapping, beard swapping and so on, as in the examples above.

The architecture consists of two modules: a segmentation module and a reconstruction module. The segmentation module segments an image (i.e. both source frame and target frame) into $K$ parts ($K$ is a fixed parameter throughout) plus background and outputs an affine transformation for each segment, corresponding to its motion.

In the reconstruction module, the motion of each segment is combined with the segmentation to obtain the optical flow between the source and the target. This flow is later applied to the source image in order to obtain the reconstruction of the target frame.

In the following we discuss both modules in more detail.

Segmentation module

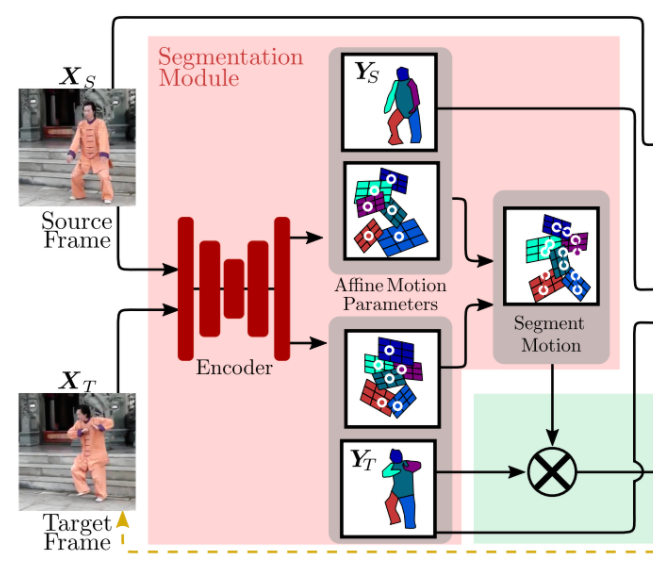
Initially, an hourglass network (aka U-Net, convolution layers followed by upconvolution layers with skip connections, for details see [6]) is applied to process the input image.

The first part of the output consists of $K+1$ masks, corresponding to $K$ segments + background (one uses softmax over channels, so masks are soft and correspond to confidence of belonging to a segment).

The second part of the output are another $K+1$ masks that are used to compute the anchor point of each segment (ones uses softmax applied to each mask separately, probabilities correspond to confidence where the anchor point is located) together with an affine transformation $\mathcal{F}$ that corresponds to the trasformation between target and source:

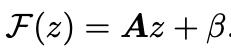
More precisely, for each segment, one estimates an affine transformation from the source to the reference image $A_T$ and from the target image to the reference image $A_S$. The reference image is an abstract entity, which is never used explicitly. It is used that the composition of the inverse of $A_T$ and $A_S$ give the desired transformation from the target image to the source image.

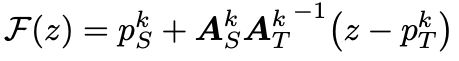
The affine transformation is, of course, just an approximation of the true transformation. What is really happening is that for each segment one simply approximates the first order Taylor expansion of the corresponding transformation. We discuss this further in "Losses" subsection below.

The affine transformations of segments are combined as a single transform in the following way

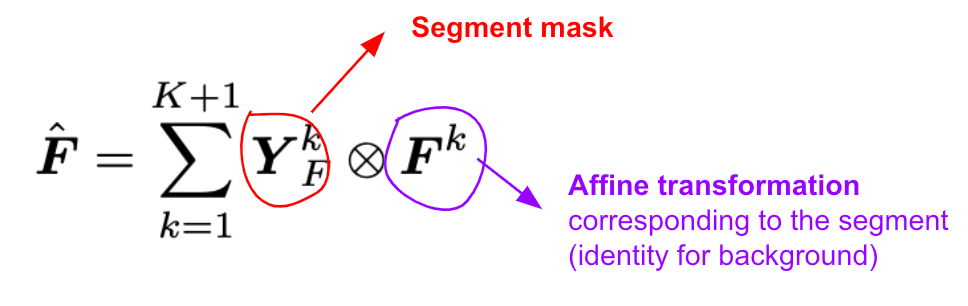
where the summation is over segments.

Reconstruction module

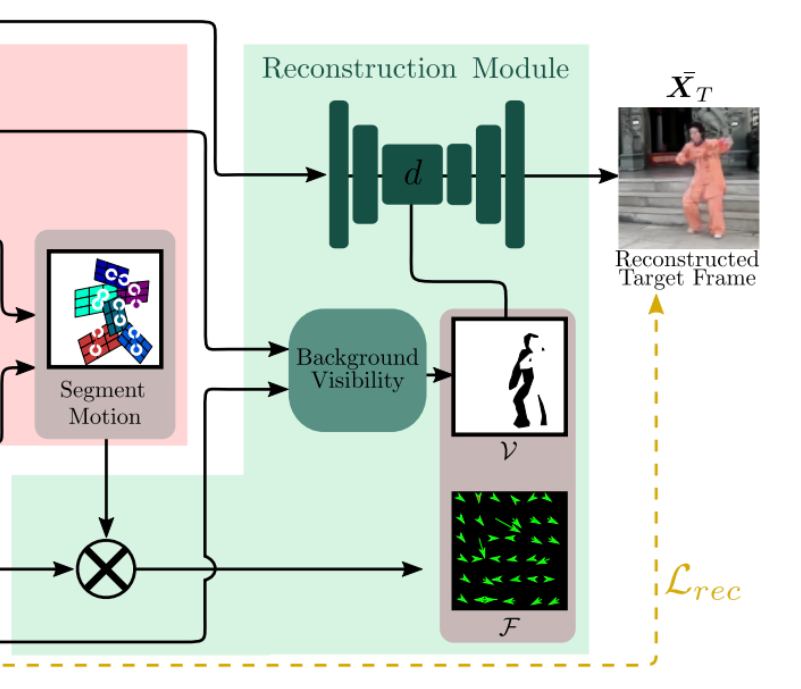
The idea of the reconstruction module is to use the computed function $\hat{F}$ to transform the source image into the target frame. Note that this operation is applied to a feature map and not to the original image.

The source image is fed in the generator network (which again has the hourglass architecture) and in the middle of the hourglass $\hat{F}$ is applied to the feature map in the following way

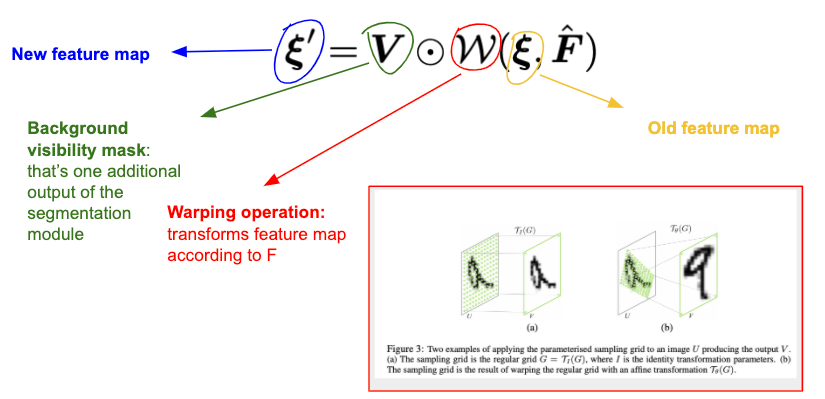
where $\xi$ is the original feature map, $\xi'$ is the new feature map and $\mathcal{W}$ is the warping operation from Spatial Transformer Networks paper [5], which transforms $\xi$ according to $\hat{F}$. Note that implementing $\mathcal{W}$ is not trivial (what does it exactly mean to apply an optical flow to an image and how to utilize GPU for that?), see [5] for details. It's available, for example, in torch.nn. The background visibility mask $V$ is yet another output of the segmentation module and predicts which pixels of the background are occluded because of the motion. In other words, the occluded pixels are simply the ones that belong to one of the foreground segments of the source image and belong to the background segment of the target image. Multiplying by this mask one simply does not allow the non-visible features to impact the reconstruction.

Losses

Two types of losses are used to train the model. The first one is the so-called reconstruction loss and controls wherever the output has similar visual features to the desired output, which is a common trick in problems such like super-resolution, colorization or style transfer. The loss is defined as follows

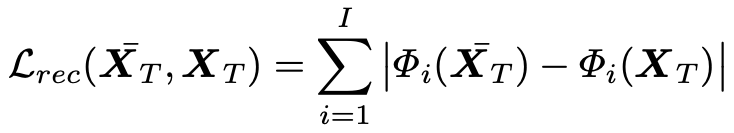
where $\Phi_i(\cdot)$ is the $i$-th channel of a specific VGG layer.

Another loss that is used is the equivariance loss. So far, we have been talking about “affine transformations” that are used to "move segments” of the source image, but of course this is just the desired outcome and the transformations were otherwise unconstrained. The equivariance loss is the key ingredient in unsupervised keypoint detection that constraints the transformations in the following way: one uses the fact that the output affine transform of the segmentation module should be robust to composition with random deformations (random in a certain class, more precisely in the class of thin spline transformations), so that it should hold that

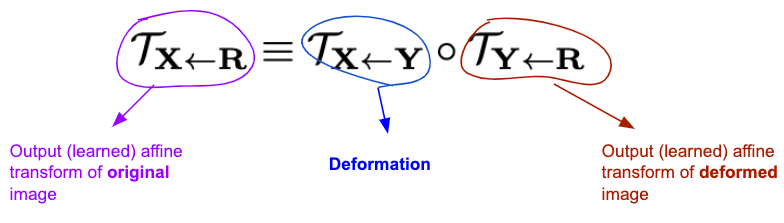
Using the Taylor expansion one approximates transformations by affine transformation $F(z) \approx F(p) + F'(p)(z - p)$, hence the equality should hold for $F(p)$ and for $F'(p)$. By the way, this is why [1] is called the first order model: because of the derivative $F'(p)$. Comparing the Taylor expansions on both sides of the above equality one wishes to (approximately) have

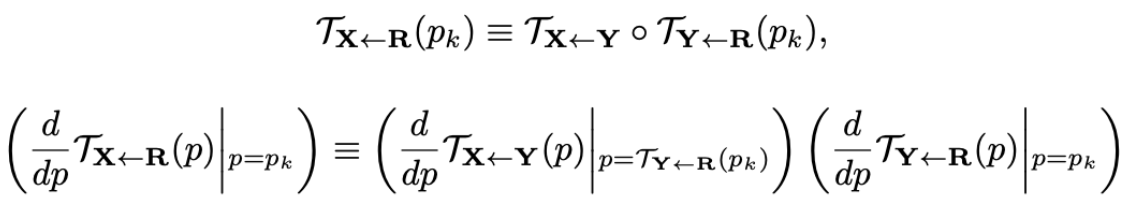
for all $p_k$, where $p_k$ is the anchor point of the $k$-th segment. One applies $L_1$ loss to the difference of the left and right hand side of the first equation and to the difference of the identity matrix and the inverse of left hand side multiplied by the right hand of the second equation (product instead of difference because of numerical stability).

First Order Motion Model For Image Animation

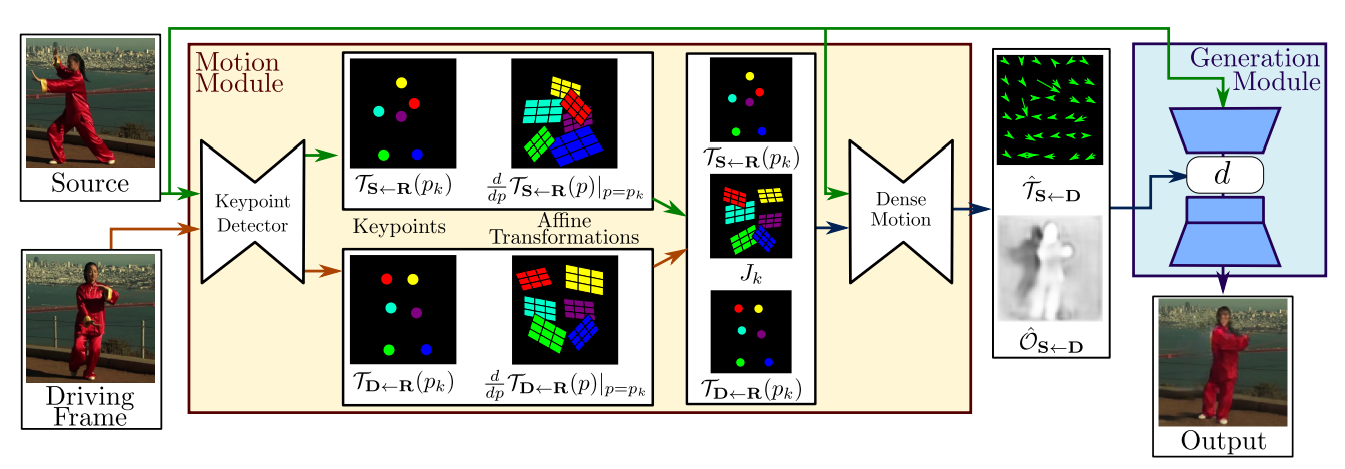
[2] is based on ideas that appeared already in [1]. The first order motion model uses a motion module, which outputs the keypoints and its corresponding transformations, but no segmentations masks per se. Note that segmentation has to still be done implicitly though, since “moving a keypoint” corresponds to “moving its neighbourhood” at the same time. The output of the motion module is then applied in a similar way to the one described above to transform the source image into the target frame.

References

[1] Siarohin, Aliaksandr, et al. "First order motion model for image animation." Advances in Neural Information Processing Systems. 2019.
[2] Lathuilière, Stéphane, et al. "Motion-supervised Co-Part Segmentation." arXiv preprint arXiv:2004.03234 (2020).
[3] https://github.com/AliaksandrSiarohin/first-order-model
[4] https://github.com/AliaksandrSiarohin/motion-cosegmentation
[5] Jaderberg, Max, Karen Simonyan, and Andrew Zisserman. "Spatial transformer networks." Advances in neural information processing systems. 2015.
[6] Ronneberger, Olaf, Philipp Fischer, and Thomas Brox. "U-net: Convolutional networks for biomedical image segmentation." International Conference on Medical image computing and computer-assisted intervention. Springer, Cham, 2015.