Game Character Customization

Often RPG games support a character creation system (Skyrim, Word of Warcraft, Dark Souls, Nioh, Knights of the Old Republic, Dragon Age, Fallout…) that allows users to create their in-game character representation in game. It’s not a rare situation in which players spend multiple hours creating and customizing their character defining every detail available. This also leads to some hilarious and impressive results like creating Arnold’s Conan in Skyrim or creating Daenerys Targaryen in Dragon Age : Inquisition. Detailed character creation feature improves player immersion, makes game experience more emotinal and customized and generally plays a very important aspect of RPG games.

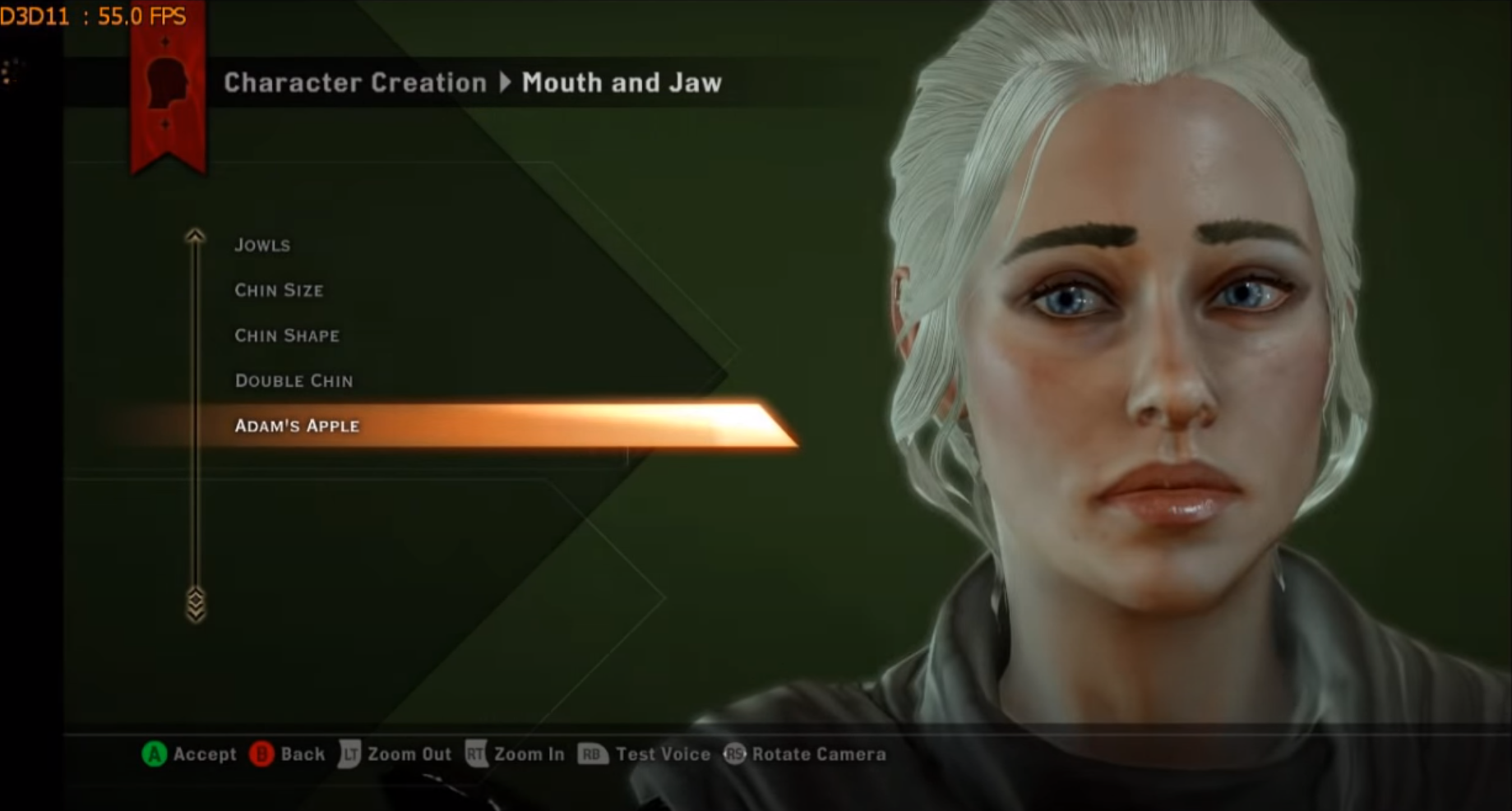
On the other hand, almost any game that has NPCs often needs many different faces that can be used to create diversity among NPCs. It is possible to conclude that a character/face editor of some sort is often a basic requirement for a game that has a need for multiple NPCs.

In this post, we will focus on talk held at GDC 20 for a MMORPG game called Justice by NetEase currently published in China. You can find a nice review about the game here, and you can see beautiful overview of graphics from the game here. Authors presented an algorithm that can be used to generate an in-game rendered face for a character from a given input image (from real life). Most of the images are taken directly from their paper and presentation from GDC.

Key Concepts

Paper proposes and evaluates an algorithm that can be used to generate and render a character face in a video game from a picture of a person (from real world).  It utilizes deep learning and a custom optimization algorithm to find a required face. Rest of the text will give an overview and explanation of the methodology, results and algorithm used to solve this problem.

Goal

Goal is to generate a set of parameters (encoded in vector x) that can be used to render an 3d face in the game engine based on the input photo. Players can continue editing created face through the game as part of their playing experience.

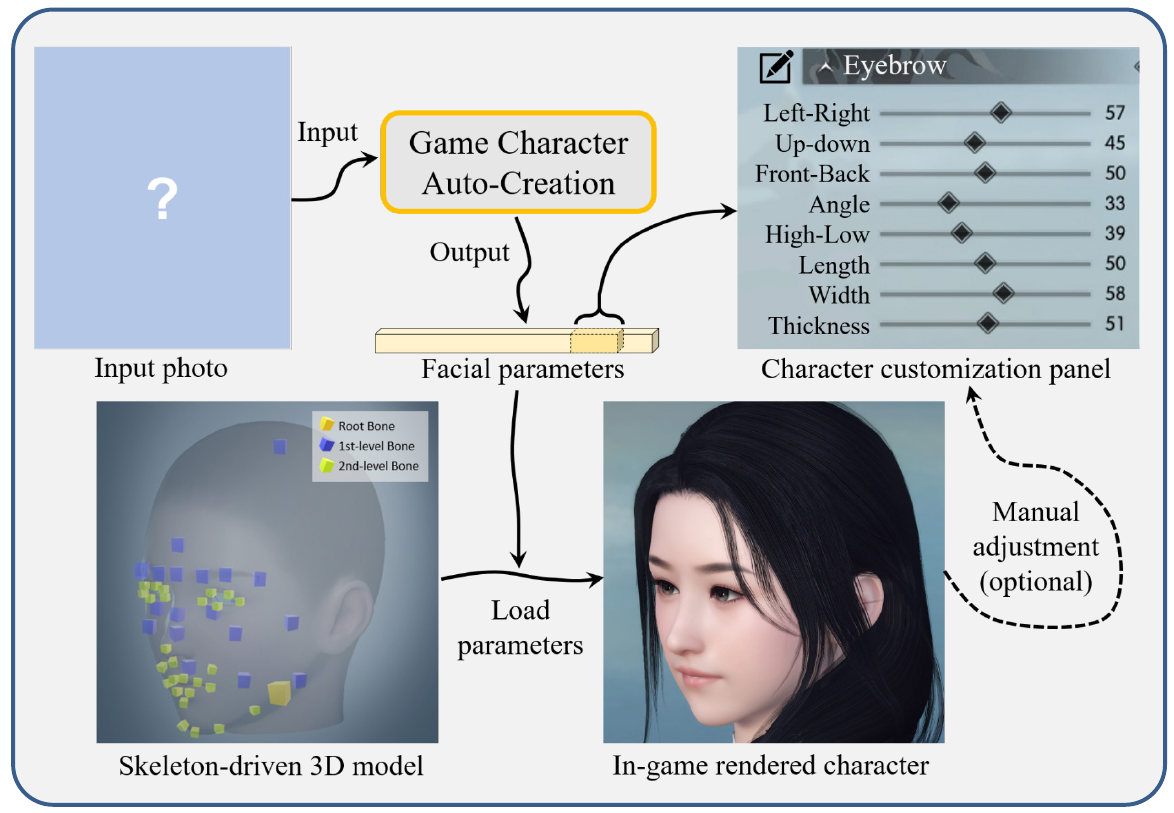
Face-to-Parameter Translation

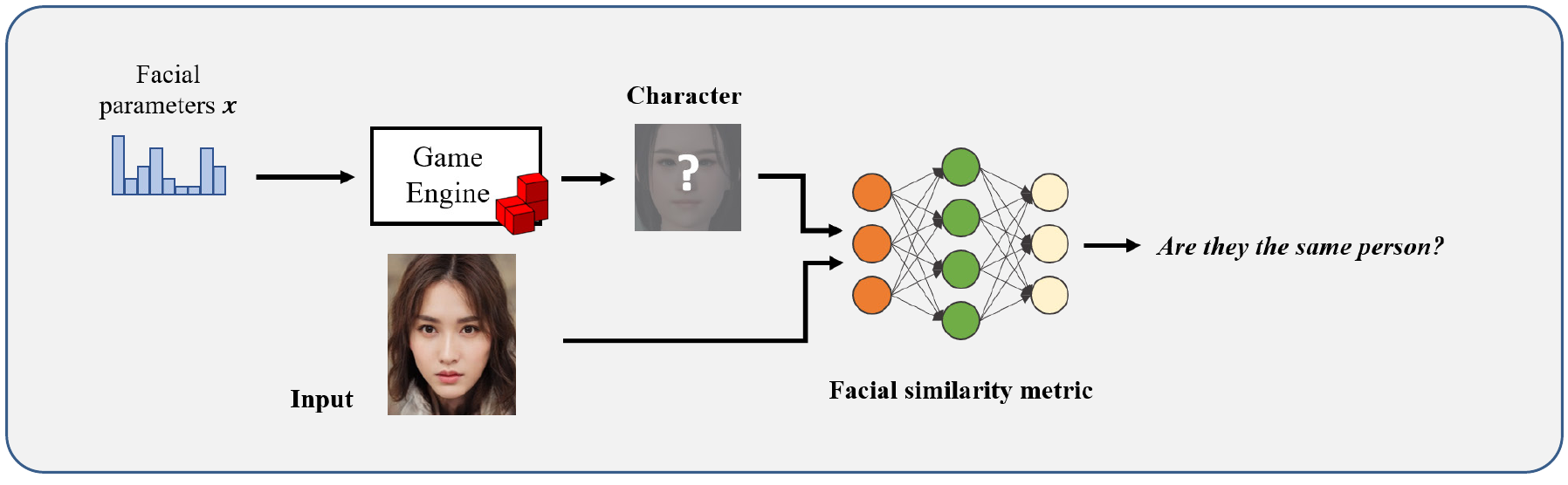
Basic approach would be to create a neural network which would try to calculate a similarity measure between an in game face and a real face, but because in-game face in rendered by using a game engine, it becomes difficult to apply deep learning and optimization algorithms directly. For those reasons, a new methodology is proposed that consists of two parts:

• Phase 1: Imitation learning model
• Phase 2: Image-to-parameter translation model

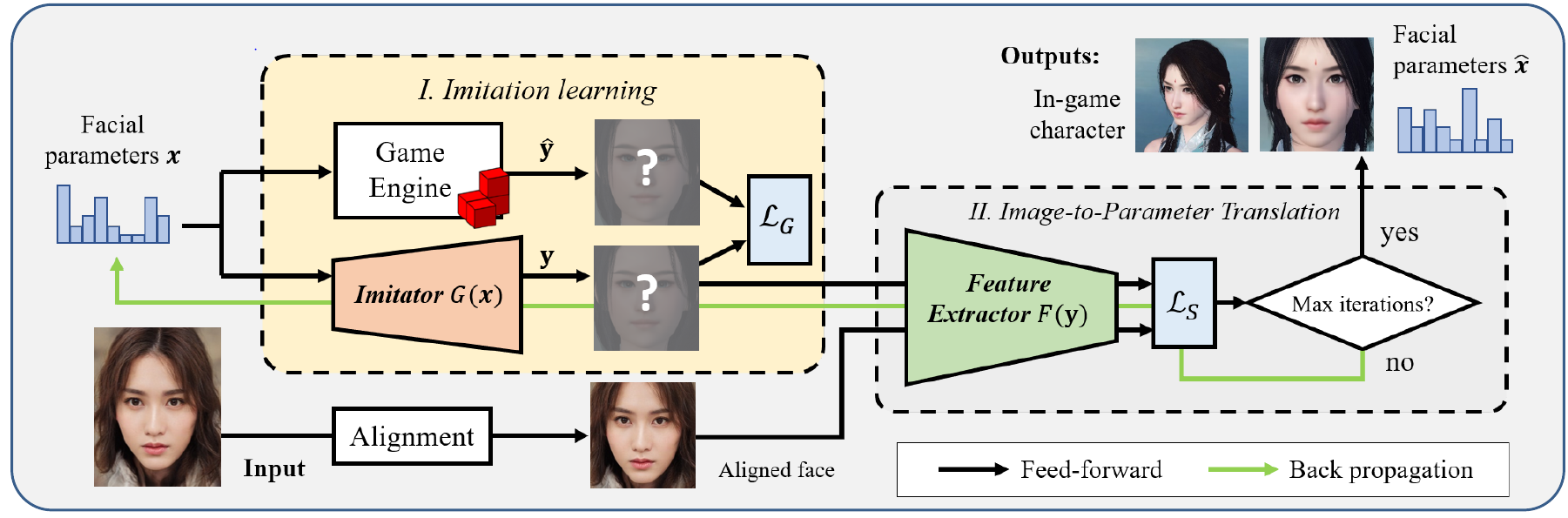
Methodology

Phase 1: Imitation learning

Idea is to create a generative neural network which will learn how to render images like game engine does from a given feature vector x. Vector x in the vector that contains encoded information about the character to be rendered in the game engine (positions and scales of different bones, types of hairstyle, eyebrows and similar).

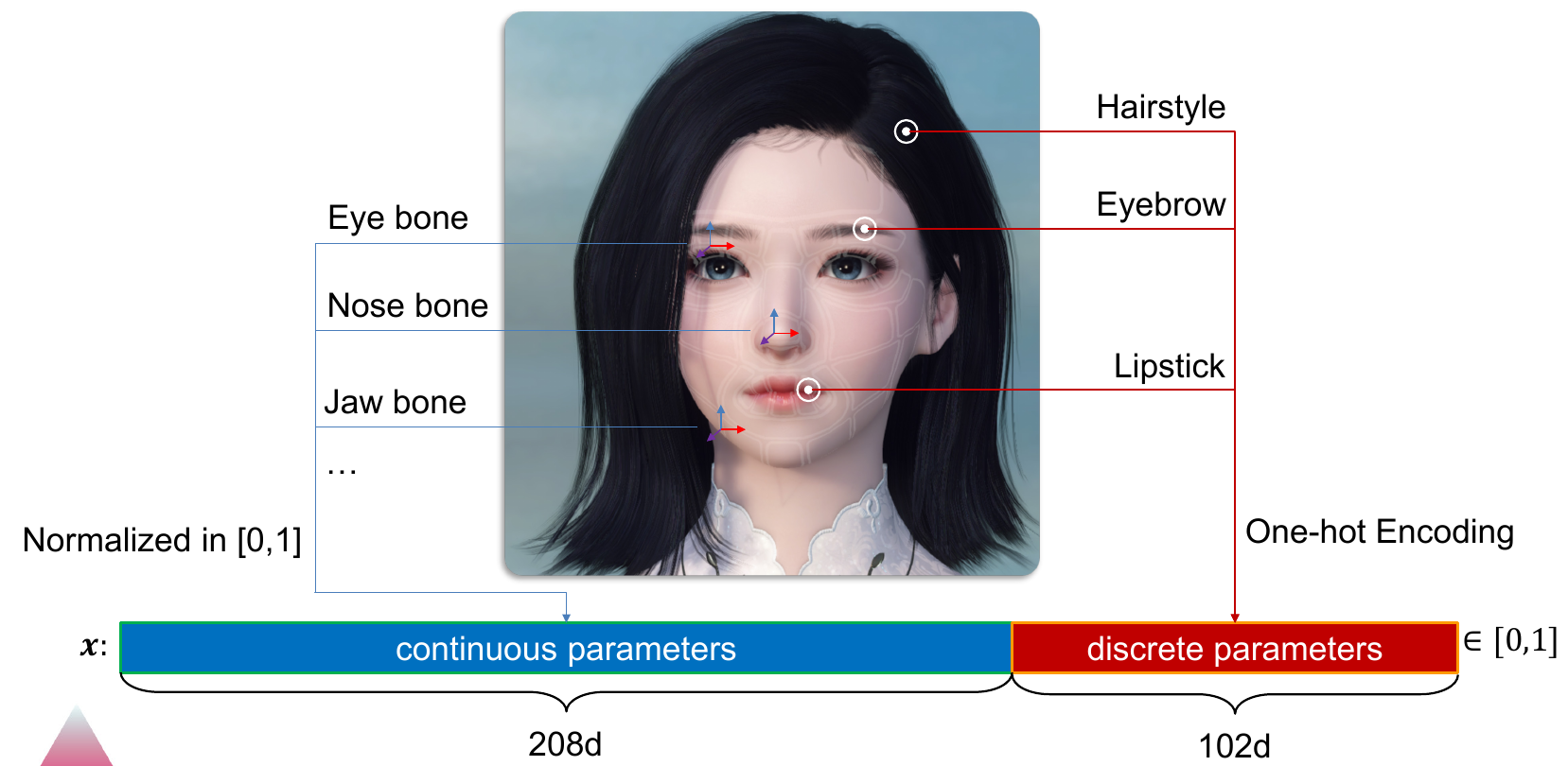
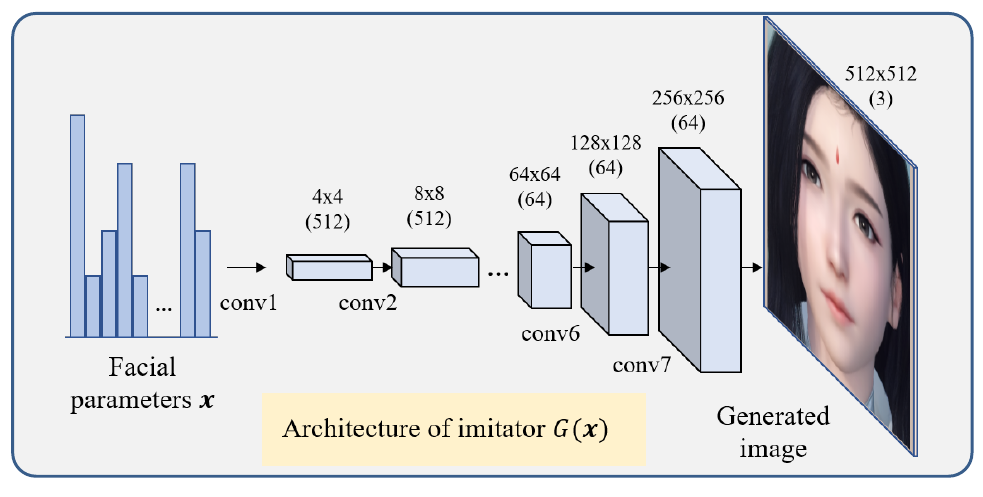
Paper has created an DCGAN [2] inspired generative network with the following notable changes:

• Input: facial parameters (208+102 dimensional vector x)
• Output: game character facial image (G(x), $512 \times 512 \times 3$ image)
• 8 transposed convolution layers attached with ReLU and BN layers
• Feature size doubled after each convolution layer

This generator (imitator) is trained in a supervised fashion. Dataset that this model is trained on is obtained by sampling 20 000 different x vectors (uniform distribution used) and rendering images through game engine to obtain ground truth (labels). Note that this doesn’t require manual labeling.

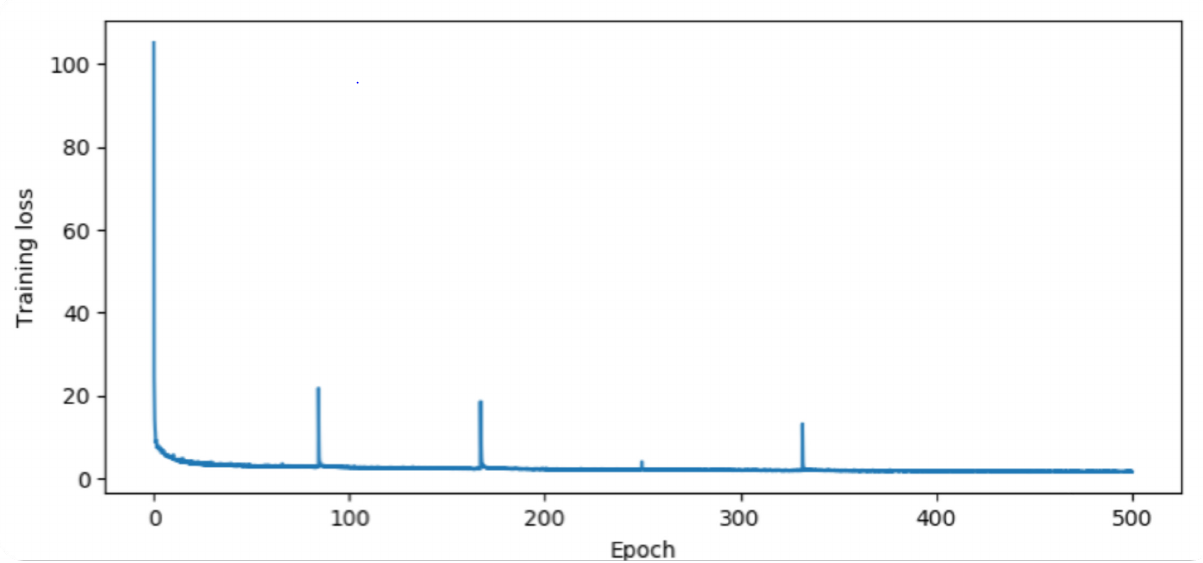
As mentioned, model is trained in a supervised fashion with following optimization configuration:

Optimizer: Stochastic Gradient Descent with momentum

• learning rate: 0.01
• momentum = 0.9
• batch size = 16
• maximum epoch = 500
• learning rate decay = 10% per epoch

Target function:

$$ \min_G E_{x \sim u(\mathbf{x})} [ || G(\mathbf{x}) - Engine(\mathbf{x}) ||_1 ] $$

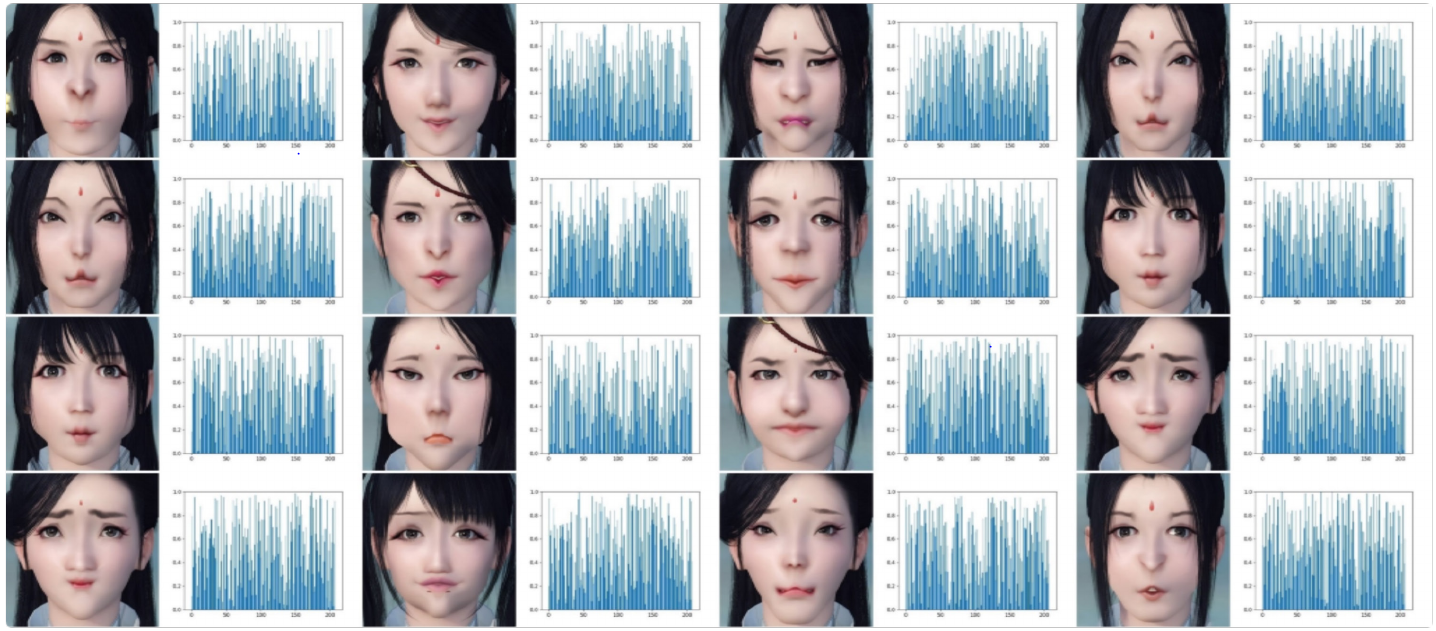
After training is complete, here are the reported results.

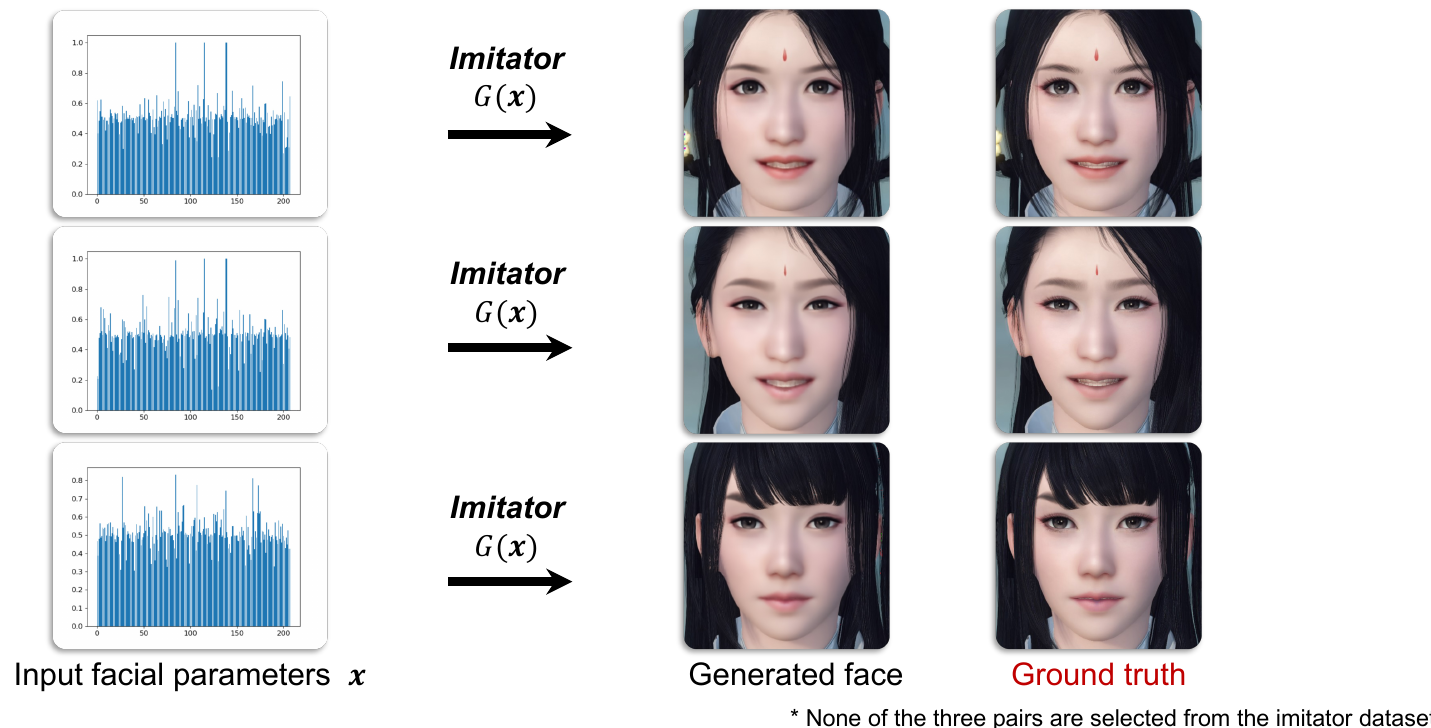
Phase 2: Face-to-parameter Translation

Next, a model is constructed that helps to model human face perception and measure face similarity. Model gets as an input 2 images that should be compared. It consists of two models:

• Face recognition model F1 (based on [3])
• Face segmentation model F2 (inspired by Resnet 50 [4])

Overall, an input of facial photo ($y_r$) and generated image (G(x)) is given and for output, losses $\mathcal{L}_1$ (identity loss) and $\mathcal{L}_2$ (content loss) are calculated.

F1 model (face recognition)

Idea is to use a pre-trained neural network for face recognition which allows to embed input images into a vector space of dimension D (256d was used in the paper as in original [3]). When images are embeded, their representations (vectors) can be compared using cosine distance. Network was trained in such a way that if input photos are photos of the same person, their embedings will be close in the resulting vector space.

Some information about the model:

• Pretrained on LFW (labeled faces in the wild)
• Input: two $128 \times 128$ grayscale images
• Output: 256d facial embedings for both images

Identity loss ($\mathcal{L}_1$) is defined as follows:

$$ \mathcal{L}_1(\mathbf{x}) = 1 - cos<F_1(\mathbf{y}_r), F_1(G(\mathbf{x}))> $$

F2 model (face segmentation)

F2 model is used to extract and obtain face information from an input image. It is a convolutional neural network based on resnet50 network. Last layer from resnet50 is replaced with 1x1 convolution layer and output resolution is increased from 1/32 to 1/8.

• Input: $256 \times 256 \times3$ image
• Output: facial features and semantic segmentation image

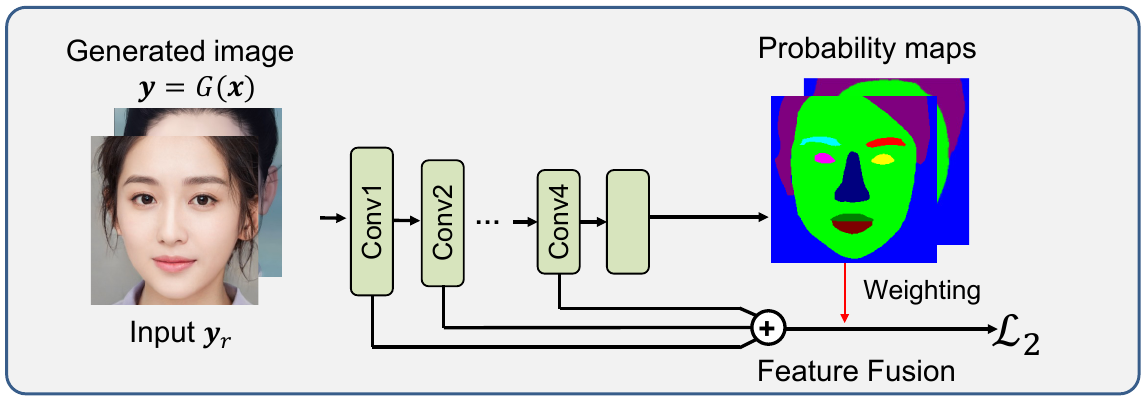
To train F2 model, Helen dataset is used which consists of large number of human photos with fine label in terms of facial features. Data augmentation is also performed (scaling, shifting…).

Training is performed in a similar fashion compared to the imitator (generative network) with the exception of a different learning rate (0.001) and a different loss function. Pixel-wise cross-entropy loss is used for image segmentation:

$$ L_{CE} = - \sum_{i=1}^K y_i \log p_i $$

Finally, $\mathcal{L}_2$  loss is defined as follows:

$$ \mathcal{L}_2(\mathbf{x}) = || F_2(\mathbf{y}_r) - F_2(G(\mathbf{x})) ||_1 $$

Final algorithm

Overall loss function $ \mathcal{L}_s $ is defined as follows:

$$ \mathcal{L}_s = \alpha \mathcal{L}_1 + \mathcal{L}_2 $$

Optimization problem is defined as follows:

$$ \min_{x} \mathcal{L}_s (\mathbf{x}) $$

Parameters can be updated in the following way:

$$ x_i = x_{i-1} - \eta \frac{\partial \mathcal{L}_s(x_{i-1})}{\partial x_{i-1}}, \ \ i = 1, 2, ..., i_{max} $$

And gradients can be computed as follows:

$$ \frac{\partial \mathcal{L}_s(x)}{\partial x} = \alpha \frac{\partial \mathcal{L}_1(x)}{\partial x} + \frac{\partial \mathcal{L}_2(x)}{\partial x} $$

$$ \frac{\partial \mathcal{L}_1(x)}{\partial x} = \frac{\partial \mathcal{L}_1(x)}{\partial F_1(G(x))} \frac{\partial F_1(G(x))}{\partial G(x)} \frac{\partial G(x)}{\partial x} $$

$$ \frac{\partial \mathcal{L}_2(x)}{\partial x} = \frac{\partial \mathcal{L}_2(x)}{\partial F_2(G(x))} \frac{\partial F_2(G(x))}{\partial G(x)} \frac{\partial G(x)}{\partial x} $$

Problem can be also looked at as a face manifold searching for a value that solves the following optimization problem:

$$ \min_x \alpha (1 - cos<F_1(y_r), F_1(y)>) + ||F_2(y_r) - F_2(y) ||_1, \ \ s.t.\ \ y = G(x) $$

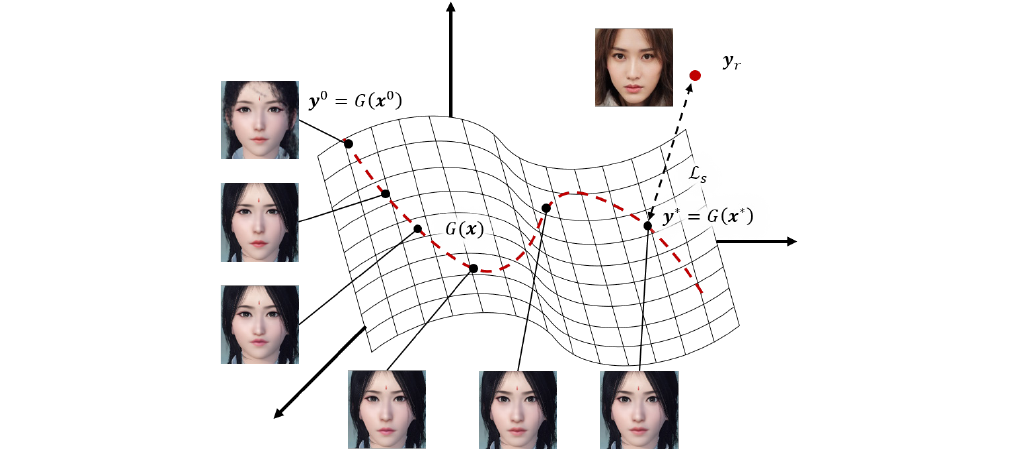
So, to perform character auto creation paper proposes the following algorithm

• Step 1: Align the user-uploaded photo based on a default game face
• Step 2: Finding optimal parameters for face
  • Step 2.1: Freeze all networks (G, F1, F2), initialize $x = x_0$, set learning rate = 10, max iterations = 10
  • Step 2.2: Use gradient descent method to update $x$
  • Step 2.3: Upon reaching max itearations, output optimized facial parameters x'
• Step 3: Render game character in the game from vector $x'$

As character creation tool allows users to edit characters, generated character can further be edited by the user.

Environment and performance

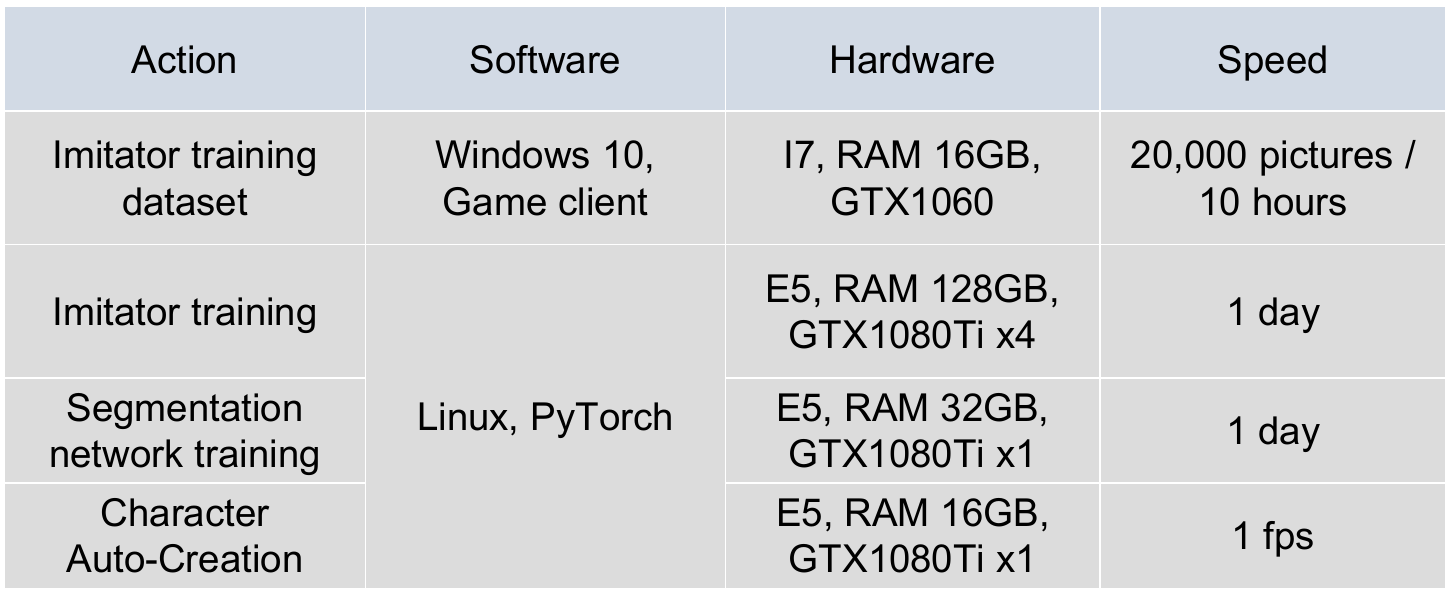
Some results

Conclusion

Advantages:

• No labeled character data is required
• The generative network can easily fit the behavior of game engine regardless of the renderer type and 3D model structure
• Deep learning based features can represent human perception on face similarity evaluation
  Limitations

Limitations:

• Sensitive to the pose, obstacle, etc.
• Discrete parameters are not well solved
• Human-like 3D model is required

Use Cases

We could use ideas from this paper in situations very similar to the use case reported in the paper:

• Allow users to generate face from their picture
• Generate celebrities in our game from their pictures

Of course, this can be done if our game/engine supports a character editor.

Resources

[1] Face-to-Parameter Translation for Game Character Auto-Creation, Tianyang Shi, Yi Yuan, Changjie Fan, Zhengxia Zou, Zhenwei Shi, Yong Liu

[2] Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks, Alec Radford, Luke Metz, Soumith Chintala

[3] A Light CNN for Deep Face Representation with Noisy Labels, Xiang Wu, Ran He, Zhenan Sun, Tieniu Tan

[4] Deep Residual Learning for Image Recognition, Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun

Also add link to code repo, if the paper has one.