Paper insights are short overviews of selected papers, read by and presented by our team members. Academic credit goes to the original authors.

MuZero [1] is a new reinforcement learning algorithm that shares many concepts with AlphaZero [2]. It achieves state-of-the-art results in Atari benchmarks, and matches (and slightly surpasses) performance of AlphaZero in chess, shogi and go. It does all of this with greater sample efficiency and, consequently, in less training time.

TwoMinutePapers has a great short overview of this paper, with focus on results achieved.

Like AlphaZero, MuZero uses Monte Carlo tree search algorithm in order to evaluate the best action during rollouts. However, unlike Alpha Zero, MuZero learns the model, i.e. has no access to game simulator, or game rules. It uses a hidden state to represent game state in tree nodes. This hidden state is a learned function of previous state(s) and a candidate action.

Game simulator allows the algorithm to compute the exact game state that will follow a specific move. Tree-search based algorithms, like MCTS, unroll future game states from the current state by trying out different moves. Overall score of each possible move in current state depends on how favorable child states stemming from that specific move are for the player. In order to assess how favorable a game state is, it is important to have accurate state prediction. In games where we have access to game rules, like chess or go, tree search yields perfect game state representation in each tree node. We say that these kinds of algorithms are model-based, because they have inherent access to game rules and game internals.

This is the first time that MCTS algorithm was employed to play Atari games, which was previously not possible because of model requirements.

In case you want to learn a bit more about Monte Carlo tree search works, check out this tutorial.

How MuZero represents state

Rather than representing actual game state - think chess board with positions of all pieces, or Atari game screenshot - MuZero learns to represent hiddent state. It is difficult to tell whether this hidden state can be interpreted in terms of actual game state, much like interpreting MLP layer activations in object detection networks. In spite of this, it captures vital information about current and previous game states, and MuZero uses it to expand the game tree. This is called the rollout phase, and is performed at each time step (or move).

MuZero learns three specific functions (subscripts denote actual rollout time steps, superscripts denote tree search iteration):

  1. representation function, $h(0_1, o_2, \ldots, o_t)$ is used to generate an initial hidden state $s^0$ at time step $t$, given previous and current observations
  2. dynamics function, $g(s^{k-1}, a^k)$ is used to generate next hidden state $s^k$ and predicts immediate reward $r^k$
  3. prediction function uses hidden state $s^k$ to predict policy $p^k$ and value function $v^k$
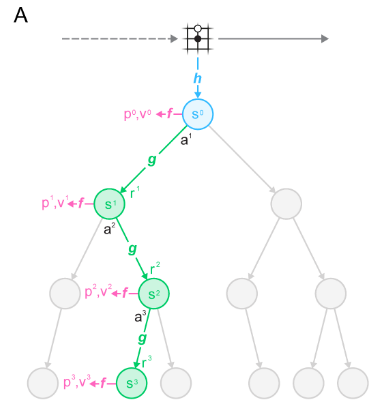
Example of rollout phase of the algorithm, taken without modification from the paper [1]

How rollouts are performed

  1. MuZero uses representation function to generate initial hidden state at current time step - this corresponds to the blue node in graph above.
  2. Next, it uses prediction function to estimate policy and value functions corresponding to that hidden state.
  3. Using predicted policy, candidate actions are sampled and tree is rolled out further by using the dynamics function to generate next tree node (green nodes) and predict immediate rewards.
  4. Steps 2-3 are repeated for each tree node during tree expansion. Tree is expanded only to some depth.

How actions are sampled

After tree has been rolled out to some depth, actual action is sampled from search policy πt, which is proportional to the visit count for each action from the root node. Environment receives this action and generates next observation ot+1 and reward ut+1. After end of each episode, trajectory data is stored into a replay buffer.

How training is performed

All three functions are trained jointly, end-to-end, by backprop through time. This is also done recurrently, as search tree unrolled at step $t$ is used to train functions at the same step and subsequent steps, up to tree depth steps in advance. Policy $p^k$ is minimized with respect to $\pi_{t+k}$, value function $v^k$ is minimized with respect to sample return $z_{t+k}$ (sample return is either n-step return in Atari games or final reward in board games), and, finally, predicted immediate reward $r_{t+k}$ is minimized with respect to actual reward $u_{t+k}$. During training, hidden state from previous tree level $s^{k-1}$ and and an actual action $a_{t+k}$ are used as input to dynamics function.

Results

MuZero outperforms existing RL model-free algorithms in Atari games, and achieves AlphaZero level of performance in chess, go (slightly outperforming AtariZero here) and shogi, and, of course, greatly outperforms humans.

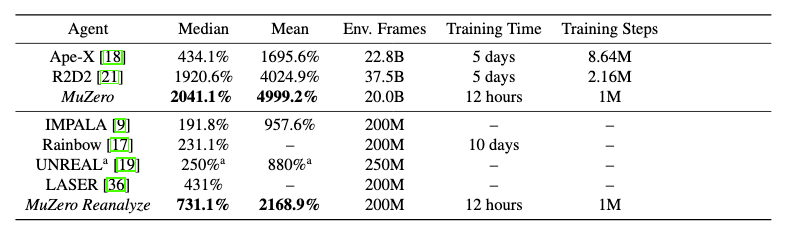
Table showing aggregated scores versus existing RL algorithms in Atari games, taken without modification from the paper [1]

Percentage scores in first two columns are with reference to human performance. One thing that stands out in table above is great sample efficiency, which leads to short training times, especially when compared to RL algorithms.

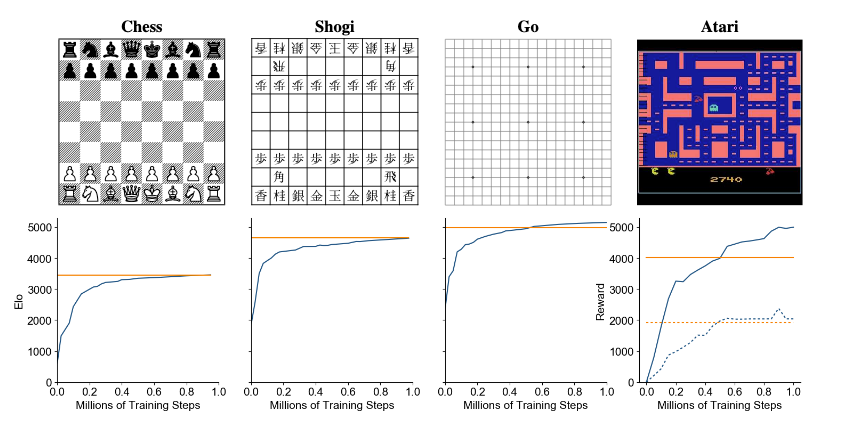
Training performance of MuZero in board and Atari games (blue line). Horizontal orange line in board games is AlphaZero's best achieved ELO. Horizontal orange line in Atari games is previous state of the art algorihtm (R2D2).

What is also shocking here is the degree to which MuZero can generalize. Even without any knowledge of Go, any notion of game rules, or board state, it is able to achieve and beat performance of Alpha Zero, and then, without any changes to algorithm internals or architecture, also beat R2D2 in Atari games, which are conceptually completely different from board games.

Use Cases

MuZero combines power of MCTS with generalization and flexibility of deep learning, and this allows us to use it in almost any video and/or board game. Its primary selling points are state-of-the-art performance and sample efficiency. It is a great choice in cases when game simulator is not available, or when accurate game state simulation during tree rollout is too costly.

References

[1] J. Schrittwieser et al., “Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model,” arXiv:1911.08265 [cs, stat], Feb. 2020 [Online]. Available: http://arxiv.org/abs/1911.08265.

[2] D. Silver et al., “Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm,” arXiv:1712.01815 [cs], Dec. 2017 [Online]. Available: http://arxiv.org/abs/1712.01815.